Brute Force / 순열 / 조합 / 멱집합
1. Brute Force
: 무작정 가능한 모든 경우를 다 검사하는 알고리즘.
ex. 4자리의 숫자로 이뤄진 비밀번호를 구해야 한다.... > 0000~9999까지 모두 해본다...?
방법은 간단하다.
모든 경우의 수를 확인해 보는 것...!
그러나, 경우의 수가 늘어나기 시작하면 수행속도가 느려지기 시작한다...
그렇지만 해답을 못 찾은 가능성이 적으므로 절! 대! 모르겠으면 일단 접근해볼 수 있는 방법이다.
2. 순열
: 서로 다른 것들 중 몇 개를 뽑아서 한줄로 나열하는 것.
서로 다른 n개 중 r개를 꺼낼 때 만들 수 있는 순열의 갯수는.......? (n개 중에서 r개 고르기)

- r = n인 경우 (n개 중에서 n개 고르기) > n 팩토리얼 (n!)
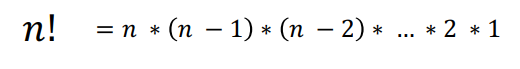
- nPr을 팩토리얼을 이용해 표현

~> n과 r의 크기가 커지면 연산 과정이 폭발적으로 증가하게 된다..

- 일단 간단하게 순열을 제작해보았다. (0부터 2까지의 숫자로 만들 수 있는 숫자나열을 전부 호출하는 메서드.)
public class Permutation {
public static void main(String[] args) {
permSimple(3);
}
// 0-2의 숫자로 만들 수 있는 숫자 나열 전부 출력하는 메서드
public static void permSimple(int n) {
int first;
int second;
int third;
// 0부터 2사이의 숫자를 차례대로 골라본다.
for(int i=0; i<n; i++) {
// 첫번째 숫자를 골랐음.
first = i;
for (int j=0; j<n; j++) {
// 이미 고른 숫자라면 나머지는 실행하지 않는다.
if (j==first) continue;
second = j;
// 0에서 2사이의 숫자 중, 아직 고르지 않은 숫자를 골라본다.
for (int k=0; k<n; k++) {
if (k==first || k==second) continue;
third = k;
System.out.println(first+" "+second+" "+third);
}
}
}
}
}
그런데, 여기서 숫자를 더 골라보고 싶다면....? 즉, nPr에서 r이 늘어난다면
그만큼 반복문(for문)이 점점 더 늘어나게 된다. > 이 반복문의 갯수가 r에 따라 달라지기 때문에 for문을 동적으로 만들어주어야 한다.
>> 그러면 이 때 반복문을 대신하여 재귀함수를 사용한다면 훨씬 좋다!!
import java.util.Arrays;
public class Permutation {
public static void main(String[] args) {
permRecursive(5,3);
}
// 재귀함수로 더 많은 원소를 선택하는 순열을 만들어보자.
public static void permRecurHelper(
// 순열을 구할때 필요한거: 고르는 대상, 고르는 갯수 (nPr)
// n개 원소 중에서 r개를 골라 만드는 순열 조합.
int n, int r,
// 내가 지금 몇번째 원소를 고르고 있는지 (for문 반복횟수)
int depth,
// 어떤 요소들을 사용했는지 저장하는 배열(즉 선택했다 안했다 표시)
boolean[] used,
// 결과를 저장하기 위한 배열 (조합결과) > 얘를 출력할 것이다.
int[] result
) {
// 재귀함수 탈출문 : r번 반복된다면? = depth가 r과 같아지면 중단.
if (depth == r) {
System.out.println(Arrays.toString(result));
} // 그렇지않으면 계속 반복할 것이다.
else {
// n개의 원소중 하나를 선택하는 for
for (int i = 0; i < n; i++) {
// 이미 선택했다면 스킵
if (used[i]) continue;
// 선택 안했다면?
// 선택을 할때 저장하는 것 결과 배열에 저장
result[depth] = i;
// 내가 이번에 i를 선택했다는걸 기록
used[i] = true;
// 중첩된 for 대신 재귀 호출
this.permRecurHelper(n, r, depth + 1, used, result);
// 이 i에서 출발하는 순열을 다 찾으면, 다음 i를 쓰기위해 기록 변경
used[i] = false;
}
}
}
// 사용성을 위해 실제 메서드를 분리한다. (n과 r만 있어도 실행이 되게끔)
public static void permRecursive(int n, int r) {
permRecurHelper(n, r, 0, new boolean[n], new int[r]);
}
}
- 혹은 "주어진 배열"에서 몇가지 원소를 골라 순열 생성하는 것도 가능하다.
private void permArray(
// 순열을 만들 대상 요소들 배열 numbers
int[] numbers,
// 고를 요소의 갯수
int r,
// 이번 재귀 호출이 몇번째 요소를 고르는 것인지
int k,
// 결과 저장용 배열
int[] perm,
// 사용한 요소 확인용 배열
boolean[] used
) {
// k == r 이면 순열 완성
if (k == r) {
// 결과 출력
System.out.println(Arrays.toString(perm));
}
else {
for (int i = 0; i < numbers.length; i++) {
// i가 이미 사용되었으면 건너뛴다.
if (used[i]) continue;
// 이번에 선택한 결과를 저장한다.
perm[k] = numbers[i];
// 사용했다고 기록하고,
used[i] = true;
// k를 하나 증가해 재귀 호출한다.
this.permArray(numbers, r, k + 1, perm, used);
// 재귀 호출이 끝나면 다른 숫자를 고르기 위해 기록을 원복
used[i] = false;
}
}
}
3. 조합
: 순열은 원소들 중 일부를 골라서 나열하는 것이면, 조합은 "순서 상관없이" 원소를 고르는 것!
= 서로 다른 n개의 것들 중 r개를 순서 상관없이 고르는 경우이다.



>> n==0이거나 n==r일 때, 순서를 고려하지 않기 때문에 모든 원소를 고르는 경우의 수는 단 한가지가 된다.
- 이번에도 간단한 조합을 제작해본다. (0~5까지의 숫자 중 3개의 숫자를 선택하는 경우)
int n=5;
int first;
int second;
ind third;
// i는 0부터 n-2까지 반복 (그래야 안쪽 반복문에서 선택할 요소가 남기때문에)
for(int i=0; i<n-2; i++) {
first = i;
// j는 i+1부터 n-1까지 반복
for(int j=i+1; j<n-1; j++) {
second = j;
// k는 j+1부터 n까지 반복
for (int k=j+1; k<n; k++) {
third = k;
System.out.println(first+" "+second+" "+third);
}
}
}>> 이번에도 재귀함수의 형태로 조합을 만들 수 있다. . . (훨씬 효율적이겠죠...?)
public class Combination {
public static void main(String[] args) {
combiRecursive(5,3);
}
public static void combiRecurHelper(
//몇개(n) 중에서 몇개(r)를 고를지
int n, int r,
//여태까지 몇개의 원소를 골랐는지
int depth,
// 이번에 고를지말지를 판단하는 숫자
int next,
//조합 결과를 담을 배열
int[] comb
) {
// 일단 재귀함수 탈출문 : r개를 골랐을 때.
if(depth == r) {
System.out.println(Arrays.toString(comb));
}
// next == n : 만약 내가 고르려고 고려할 애가 범위를 벗어나려고 한다면..
else if (next == n) {
return; //반환하는 값 없이 원래 실행되었던 위치로 간다.
}
else {
comb[depth] = next; //이번에 판단중인 숫자를 우선 할당한다.
// depth번째인 원소를 골랐으니까 depth+1번째 원소를 고르러 간다.
combiRecurHelper(n, r, depth+1, next+1, comb);
// next를 선택하지 않고 depth번째 원소를 판단하러 넘어간다.
// next를 선택하지 않으면 comb[depth]에 할당한 next는 덮어씌워진다.
combiRecurHelper(n, r, depth, next+1, comb);
}
}
// 사용성을 위해 실제 메서드를 분리한다. (n과 r만 있어도 실행이 되게끔)
public static void combiRecursive(int n, int r) {
combiRecurHelper(n, r, 0, 0, new int[r]);
}>> 순열에서는 순서가 중요하지만, 얘는 next에 해당하는 값을 넣을지 말지만 판단하면 된다. 그래서 boolean[] used 배열을 굳이 사용할 필요가 없음.
- 마찬가지로 특정 배열에서 선택할 때는 이렇게 표현 가능하다.
private void combArray(
int[] numbers, int r, int k, int next, int[] comb
) {
// k == r: 고를 만큼 원소를 골랐다
if (k == r) {
System.out.println(Arrays.toString(comb));
}
// next == n: 고르기 전 고를 대상이 떨어졌다
else if(next == numbers.length) {
return;
}
else {
// comb[k]에 이번에 판단중인 숫자를 우선 할당한다.
comb[k] = numbers[next];
// next를 선택하고, k + 1번째 원소를 판단하러 넘어간다.
combArray(numbers, r, k + 1, next + 1, comb);
// next를 선택하지 않고 k번째 원소를 판단하러 넘어간다.
// next를 선택하지 않으면 comb[k]에 할당한 next는 덮어씌워진다.
combArray(numbers, r, k, next + 1, comb);
}
}
** 조합이 이해가 안가 추가 설명을 찾아보다가 넣었다.
<조합 경우의 수 구하기>
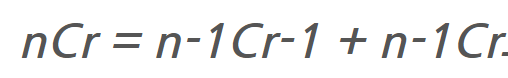
>> 조합을 이렇게도 표현하는데, 왜 그렇게 표현하는지 이해가 안됐다.
살펴보자면,
조합은 하나의 원소를 뽑는 경우와 뽑지 않는 경우의 합을 나타낸다.
ex) 5C3이라고 하자.
5개 중에서 3개를 뽑는데,
- 만약 1을 무조건 포함하고 나머지 2개를 뽑는다고 생각하면 > 4개 중에 2개 뽑기 4C2가 된다.
- 만약 1을 포함하지 않곡 뽑는다면? > 1을 빼고, 4개 중에 3개 뽑기 4C3이 된다.
>> 이 두 경우를 합치면 결국 5개중 3개를 뽑는 경우의 수가 된다. 그래서 저렇게 표현이 된 것!
그러면 이것을 코드로 구현해본다. 재귀호출에 대해 너무 이해가 안됐었다...
재귀호출은 탈출문을 먼저 생각해본다!
public class Combination {
public static void main (String[] args) {
System.out.println(combination(5,3)); //5개 중 3개 뽑는 조합의 경우의 수
}
public static int combination(int n, int r) {
if (n==r || r==0) {
return 1;
}
else {
return combination(n-1, r-1) + combination(n-1, r);
}
}
}
요 재귀함수 코드가 어떻게 돌아가는지 이해가 안되어서 그려보았다. 하나하나 계속 재귀함수를 거쳐 지나가다보면
n==r일 때 도는 r==0일 때가 끝이고, 이때 1을 리턴해서 하나하나 더해보면 결과 값이 나온다.
4. PowerSet (멱집합)
* 부분집합? : 어떤 원소의 모음인 집합에서 일부 또는 전부의 원소를 선택해 새로운 집합을 만드는 것.
- 멱집합 ? : 어떤 집합에 대하여, 해당 집합이 가질 수 있는 모든 부분집합들의 집합.
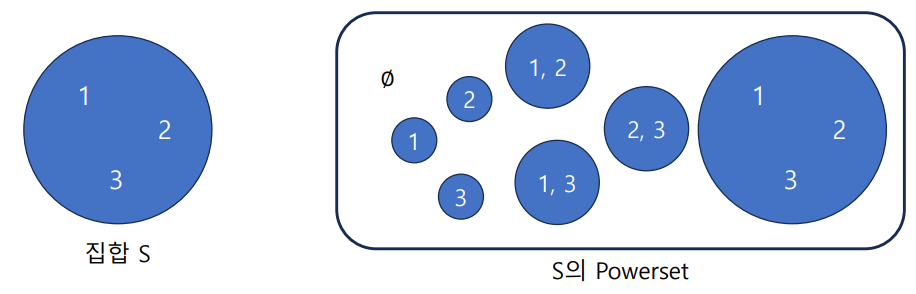
ex) 어떤 집합이 n개의 원소 가진다면 > 각각의 n에 대해서 부분집합에 포함할지 말지 결정 > 각 n개의 원소마다 2가지 경우의 수가 생김 > 총 2^n개의 부분집합이 생김!!
1) 반복문 사용
// 몇번째 원소를 선택할지 여부를 0과 1로 구분
int[] target = new int[]{2,3,5};
int[] select = new int[]{0,0,0};
for(int i=0; i<2; i++) {
//0일 경우 미선택, 1일 경우 선택
select[0] = i;
for(int j=0; j<2; j++) {
select[1] = j;
for(int k=0; k<2; k++) {
select[2] = k;
// select의 3번째 원소가 결정되면 부분집합이 완성된다.
for (int l = 0; l<3; l++) {
if(select[l] ==1) {
System.out.print(target[l]+" ");
}
System.out.println();
}
}
}
}>> 이 방법의 경우 순열/조합과 마찬가지로 대상 원소의 갯수가 많아질수록 for문도 많아지게 된다....
== 재귀함수 호출을 사용하자!!
public class PowerSetRecursive {
public static void main(String[] args) {
int[] target = new int[]{2,3,5};
new PowerSetRecursive().powerSet(target, 0, new int[target.length]);
}
public void powerSet(
int[] target, //부분집합을 생성할 대상 배열
int next, // 다음에 선택할 배열 요소의 인덱스
int[] select // 각 요소가 부분집합에 속하는지 나타내는 배열 (0이면 미선택, 1이면 선택)
) {
if (next == target.length) { //next가 배열의 길이와 같아지면
for(int i=0; i<target.length; i++) {
if (select[i] ==1) System.out.print(target[i]+" "); //1일경우 출력
}
System.out.println();
}
else { // 그렇지 않으면 현재요소를 선택하지 않고 다음 요소로 이동한 후
powerSet(target, next+1, select); //재귀함수 호출
select[next] = 1; // 현재요소를 선택하고 다음 요소로 이동한 후
powerSet(target, next+1, select); // 재귀함수 호출
select[next] = 0; // 다시 원상복귀
}
}
}
'Coding test > Algorithm' 카테고리의 다른 글
| 이항 계수 (0) | 2023.12.29 |
|---|---|
| DP(Dynamic Programming) (2) | 2023.12.28 |
| Queue 큐 / LinkedList / BFS (3) | 2023.12.07 |
| 정렬 Sorting (버블/선택/카운팅/이진 탐색) (2) | 2023.12.05 |
| 알고리즘 (3) | 2023.12.04 |













