정렬 Sorting (버블/선택/카운팅/이진 탐색)
~ 정렬 ~
: 2개 이상의 자료가 모여있을 때 특정 기준으로 작은 값부터 큰 값으로 재배열하는 행위.
1. Bubble Sort 버블정렬
: 인접한 두 자료를 비교하며 자리를 교환하는 방식 (마치 한번의 단게가 반복될때마다 큰 숫자가 위쪽 인덱스로 넘어가는 모습에서 거품이 일어나는 것 같다는 의미)
1) 첫번째 원소와 두번째 원소를 비교한다. 만약 첫번째 원소가 두번째 원소보다 더 크다면 둘의 자리 교환.
2) 두번째 원소와 세번째 원소도 동일하게 비교하고 교환. 이를 마지막 두 원소까지 반복.
>> 이렇게 한바퀴 돌면 ? 제일 큰 원소가 제일 오른쪽으로 간다.
다음에는 제일 큰 원소 제외하고 반복.
- 버블 정렬 코드
public class BubbleSort {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(" ");
int[] nums = new int[input.length];
for (int i=0; i<input.length; i++) {
nums[i] = Integer.parseInt(input[i]);
}
int max = input.length-1;
for (int i=0; i<max; i++) {
for (int j=0; j<max-i; j++) {
if (nums[j] > nums[j+1]) {
int temp = nums[j];
nums[j] = nums[j+1];
nums[j+1] = temp;
swapCheck = true;
}
}
System.out.println("round"+i+ Arrays.toString(nums));
}
for (int i : nums) {
System.out.print(i+" ");
}
}
}
>> 2라운드 때부터 이미 사실 정렬이 완료된 상태이다.... 이 정렬 횟수까지 줄이려면!!
swapCheck하는 boolean을 만들어준다.
public class BubbleSort {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(" ");
int[] nums = new int[input.length];
for (int i=0; i<input.length; i++) {
nums[i] = Integer.parseInt(input[i]);
}
int max = input.length-1;
for (int i=0; i<max; i++) {
boolean swapCheck = false;
for (int j=0; j<max-i; j++) {
if (nums[j] > nums[j+1]) {
int temp = nums[j];
nums[j] = nums[j+1];
nums[j+1] = temp;
swapCheck = true;
}
}
System.out.println("round"+i+ Arrays.toString(nums));
if (swapCheck==false) break;
}
for (int i : nums) {
System.out.print(i+" ");
}
}
}
>> 이렇게 하면 더이상 돌지 않아도 바로 결과 출력 가능.
- 시간복잡도 계산
: 한 번의 단계에서 가장 큰 숫자가 오른쪽 끝으로 정렬되게 된다. > 다음 단계에서는 오른쪽 끝 숫자는 비교 대상에서 제외됨.
총 비교 횟수는 각 단계에서 일어난 비교 횟수의 합.
N-1부터 1까지의 합이라고 볼 수 있다~~~~!

계산하면 O(N^2)로 표현할 수 있다.
2. Selection Sort 선택정렬
: 주어진 자료 중 제일 작은 숫자를 골라서 앞으로 정렬하는 방식.
1) 주어진 자료를 검색해 가장 작은 값을 찾고, 제일 앞의 원소와 교환. >> 제일 앞의 원소는 정렬된 상태
2) 정렬되지 않은 값들 중 제일 작은 값을 찾아, 또 교환.
- 선택 정렬 코드
public class SelectionSort {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(" ");
int[] nums = new int[input.length];
for (int i=0; i<input.length; i++) {
nums[i] = Integer.parseInt(input[i]);
}
int length = nums.length;
for (int i=0; i< length; i++) {
// 현재 정렬되지 않은 제일 앞쪽 원소는 i
int index = i;
// nums 원소 중 최솟값이 어디있는지를 찾는다.
for (int j=i; j<length; j++) {
if (nums[index] > nums[j]) {
index = j;
}
}
// 제일 작은 원소와 제일 앞의 원소를 교환.
int tmp = nums[index];
nums[index] = nums[i];
nums[i] = tmp;
System.out.println("round"+i+": "+ Arrays.toString(nums));
}
System.out.println(Arrays.toString(nums));
}
}- 시간 복잡도 계산
: 한번 작업을 거치면 제일 왼쪽 끝에 가장 작은 숫자가 정렬됨.
- 버블정렬과 시간 복잡도는 비슷하다. 그러나, 실제 데이터가 교환되는 횟수가 버블정렬보다 적다.
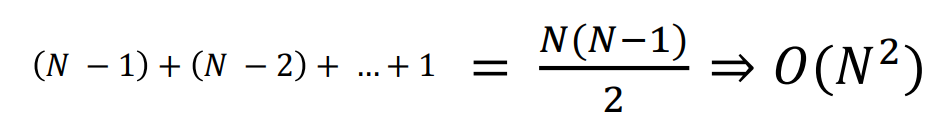
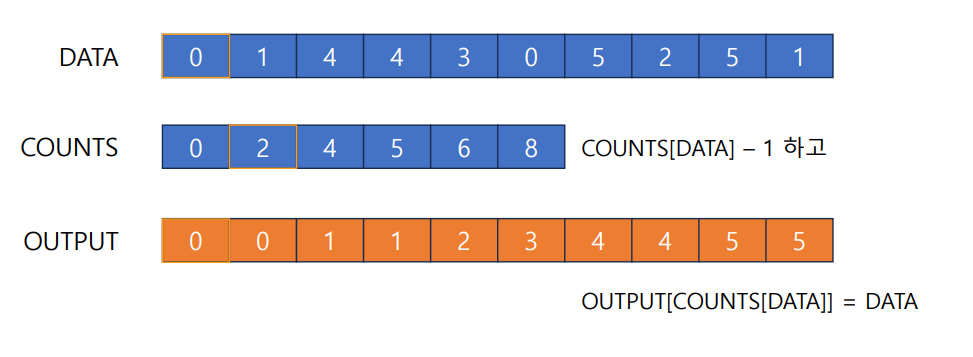
3. Counting Sort 카운팅 정렬
: 카운트 배열을 만들고, 그 결과를 바탕으로 정렬을 진행. (정렬할 자료가 정수 형태일 때 적용 가능)
각 자료가 몇개가 존재하는지를 정리한 뒤 그 정보를 활용해 정렬하는 방식.
1) 자료의 정수 최댓값 만큼의 공간을 가진 counts 배열 만들기. (counts[i] 는 i가 총 몇개인지 들어가는 배열)
2) 제일 앞쪽 원소부터 시작해 counts 배열에 index에 위치한 원소의 값을 index+1에 위치한 원소의 값에 더해줌.
3) 실제 정렬된 결과(output)을 담을 배열을 만들고, 본래의 자료를 순회함. (뒤에서부터 시작 : stable sort를 위해. 먼저 나온 숫자가 먼저 나오도록 하기 위해서)
>> counts[data] 위치의 원소를 가져옴. 이것이 index.
output[index]에 data 할당
counts[data]의 값 하나 줄이기.
자료 순회가 마무리되면 output 배열이 정렬된 결과를 갖고 있게 된다.
>> 그림 설명
- 카운팅 정렬 코드
public class CountingSort {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(" ");
int[] nums = new int[input.length];
for (int i=0; i<input.length; i++) {
nums[i] = Integer.parseInt(input[i]);
}
// 최댓값 찾기
int max = nums[0];
for (int i=1; i<nums.length; i++) {
if (max < nums[i]) {
max = nums[i];
}
}
// 배열의 크기는 최댓값
int[] counts = new int[max+1];
// nums를 돌면서 숫자 올리기
for (int i: nums) {
counts[i]++;
}
// counts 배열을 각 데이터가 마지막에 나오는 위치가 담기게 조정
for (int i=0; i<counts.length-1; i++) {
counts[i+1] += counts[i];
}
int[] output = new int[nums.length];
// 맨 마지막 nums부터 순회
for (int i=nums.length-1; i>=0; i--) {
// 현재 원소의 마지막 위치를 조정
counts[nums[i]]--;
// 현재 데이터의 다음 위치 정보를 회수
int position = counts[nums[i]];
// 새로운 배열의 position에 데이터 넣기
output[position] = nums[i];
System.out.println(Arrays.toString(output));
}
System.out.println(Arrays.toString(output));
}
}
- 시간 복잡도 계산
: 자료의 갯수가 N개이며, 최솟값이 0, 최댓값이 K일 때 계산 방법
1) 카운트 배열 만드는 단계에서 N번의 계산.
2) 카운트 배열의 값들을 누적합 하는 과정에서 배열 전체 살펴보므로 K+1번의 계산
3) 다시 전체 자료를 살피며 결과 배열 만들 때 N번의 계산
>> 종합적으로 봤을 때 O(n+k)
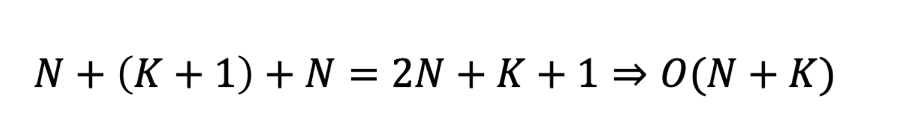
>> 특성상 자료의 총량보다 자료의 범위가 너무 크지 않을 때 효율적인 알고리즘이다.
(ex. 자료의 범위가 0~10000인데, 자료의 갯수는 10개일때..? 우우....)
4. Binary Search (이진 탐색)
: 이미 정렬된 원소의 나열에서 어떤 특정 원소를 찾기 위해 검색 범위를 절반으로 줄여가는 검색 알고리즘.
ex. 술게임.. 업앤다운.... ? ㅎㅎ
1) 가운데 위치한 원소를 고르고 비교.
2) 찾는 원소와 일치한다면 검색 성공.
찾는 원소보다 크다면? 왼쪽 절반을 다음 검색 대상으로 선택
찾는 원소보다 값이 작다면? 오른쪽 절반을 다음 검색 대상으로 선택.
3) 찾는 원소를 만나거나, 찾을 수 있는 범위가 사라졌을 때 검색을 종료

- 이진 탐색 코드
public class BinarySearch {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int searchGoal = 29;
int goalIndex = 0;
String[] input = br.readLine().split(" ");
int[] nums = new int[input.length];
for (int i=0; i<input.length; i++) {
nums[i] = Integer.parseInt(input[i]);
}
System.out.println(Arrays.toString(nums));
// 검색 대상 경계선을 세운다. =배열의 시작과 끝의 인덱스 저장
int left = 0;
int right = nums.length-1;
System.out.println(right);
boolean found = false;
while(left <= right) {
// 중간지점 설정 (왼쪽부터 오른쪽 까지의 거리의 절반만큼 왼쪽에서 출발)
int mid = left + (right - left)/2;
System.out.println(mid);
// 1. 가운데에 원하는게 있다
if (nums[mid] == searchGoal) {
goalIndex = mid;
found = true;
break;
}
// 2. 가운데가 원하는 것보다 작다. 찾아야하는게 지금보다 오른쪽이다.
else if (nums[mid] < searchGoal) {
left = mid + 1;
}
// 3. 가운데가 원하는 것보다 크다.
else {
right = mid - 1;
}
}
// 탐색에 실패했다면, 그걸 표시하기 위한 값을 반환.
if (!found) {
System.out.println("not found!");
} else {
System.out.println("goal index : "+goalIndex);
System.out.println("searchGoal : "+ nums[goalIndex]);
}
}
}

- 시간 복잡도 : O(logN)
'Coding test > Algorithm' 카테고리의 다른 글
| DP(Dynamic Programming) (2) | 2023.12.28 |
|---|---|
| Brute Force / 순열 / 조합 / 멱집합 (1) | 2023.12.17 |
| Queue 큐 / LinkedList / BFS (3) | 2023.12.07 |
| 알고리즘 (3) | 2023.12.04 |
| 정렬 알고리즘 (선택, 삽입, 버블 정렬) (0) | 2023.08.28 |