정렬 알고리즘 (선택, 삽입, 버블 정렬)

| 안정정렬 | 불안정정렬 | 제자리 정렬 |
| 버블 정렬 | 선택 정렬 | 선택 정렬 |
| 삽입 정렬 | 퀵 정렬 | 삽입 정렬 |
| 카운팅 정렬 | 병합 정렬 | |
| 병합 정렬 |
🧶정렬 시 고려사항
- 시간 복잡도
- 메모리 사용량
- 안정성(stability) : 데이터의 순서가 바뀌지 않는지 여부 (모든 정렬 알고리즘은 같은 키를 가진 데이터의 순서를 바꾸기도 함...)
- 직렬 vs. 병렬
> 항상 정답이 있는 것은 아니다!
1) 정렬할 데이터의 양
2) 데이터와 메모리
3) 이미 정렬된 정도
4) 필요한 추가 메모리의 양
5) 상대위치 보존여부 (안정성) 등에 따라 달라질 수 있다.
🤏🏻 1. 선택 정렬 (Selection Sort)
: 선택된 값과 나머지 데이터 중에 비교하여 알맞은 자리를 찾는 알고리즘.
1) 주어진 리스트에서 최솟값을 찾는다.
2) 최솟값을 맨 앞 자리의 값과 교환한다.
3) 맨 앞 자리를 제외한 나머지 값들 중 최솟값을 찾아 위와 같은 방법으로 반복한다.
public class Selection_Sort {
public static void selectionSort(int[] a) {
selectionSort(a, a.length);
}
private static void selectionSort(int[] a, int size) {
for (int i = 0; i< size-1; i++) {
int min_index = i;
// 최솟값을 갖고 있는 인덱스 찾기
for (int j = i+1; j<size; j++) {
if (a[j] < a[min_index]) {
min_index = j;
}
}
// i번째 값과 찾은 최솟값을 서로 교환 (swap함수가 없으므로 따로 구현하기)
swap(a, min_index, i);
}
}
// swap 함수 만들기 (a[i]와 a[j]를 바꾸기)
private static void swap (int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
| 장점 | 추가적인 메모리 소비가 작다. |
| 단점 | 시간복잡도가 O(N²)이다. 안정(stable) 정렬이 아니다. (안정성 보장X) |
👐🏻 2. 삽입 정렬 (Insertion Sort)
: 데이터 집합을 순회하면서 정렬이 필요한 요소를 뽑아내어 이를 다시 적당한 곳으로 삽입하는 알고리즘.
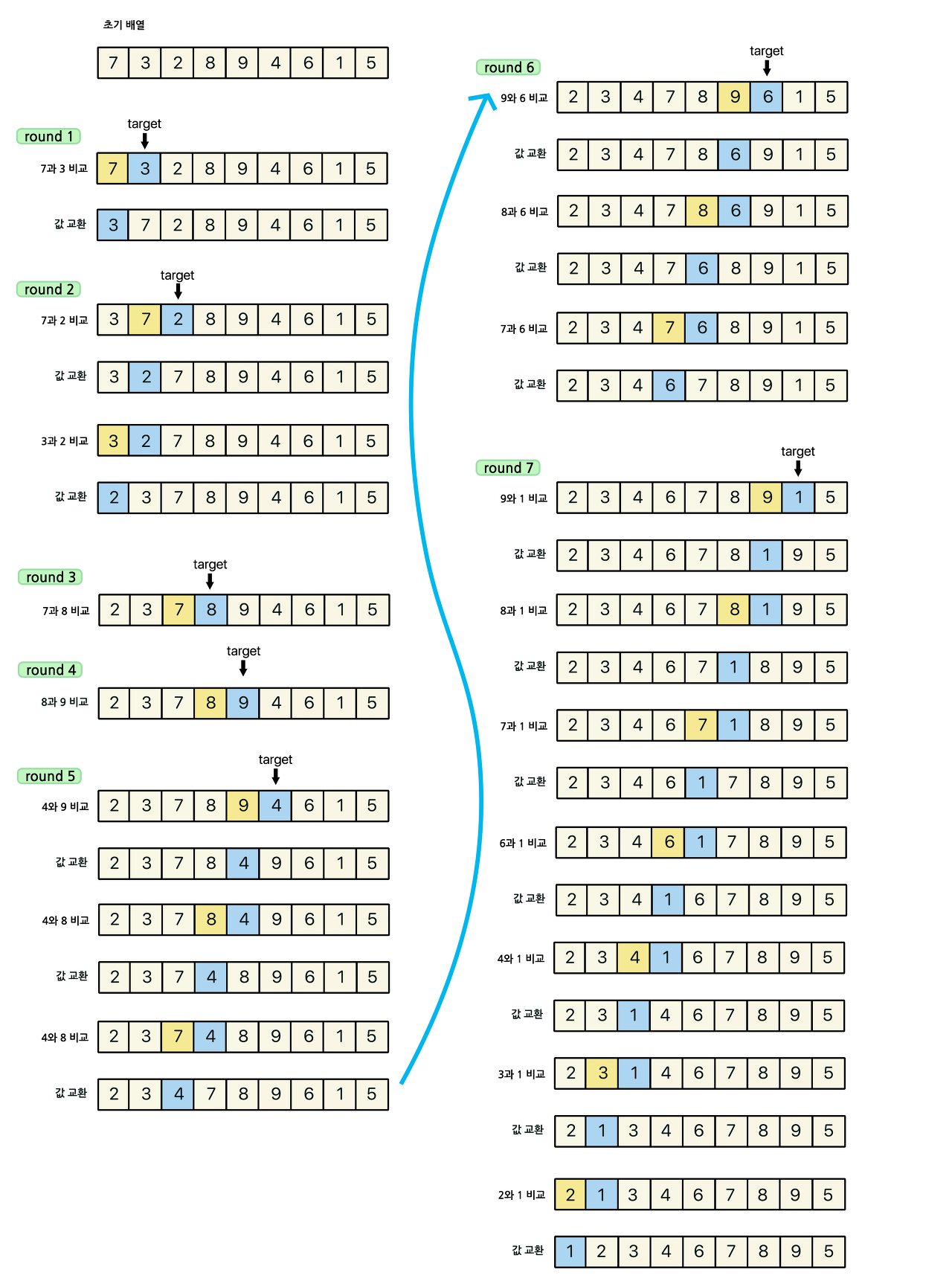
1. 현재 타겟이 되는 숫자와 이전 위치에 있는 원소들을 비교한다. (첫 번째 타겟은 두 번째 원소부터 시작한다.)
2. 타겟이 되는 숫자가 이전 위치에 있던 원소보다 작다면 위치를 서로 교환한다.
3. 그 다음 타겟을 찾아 위와 같은 방법으로 반복한다.
- 최선의 경우 시간 복잡도 O(N)/ 최악의 경우 O(N²)
public class insertionSort {
void insertionSort(int[] a, int size) {
// 순차적으로 전체 데이터를 훑기 (i는 앞에서부터 훑기)
// 0번 인덱스는 비교할 대상이 없으므로 int i를 1부터 시작해야함.
for (int i=1; i<size; i++) {
//타겟 넘버[1부터size까지]
int target = a[i];
int j= i-1; //이전원소와 비교하기 위한 변수설정
// 타겟이 이전 원소보다 크기 전까지 반복
while (j>=0 && target < a[j]) {
a[j+1] = a[j]; //이전 원소를 한 칸씩 뒤로 미룬다.
j--;
}
a[j+1] = target;
}
}
}
🧼 3. 버블 정렬 (Bubble Sort)
: 인접한 두 수를 비교하여 오름차순 or 내림차순으로 정렬 (안정성은 보장한다.)
왜 버블일까!? >> 정렬 과정에서 원소의 이동이 마치 거품이 수면 위로 올라오는 것 같아서!!
- 제자리 정렬 (in-place sort): 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에
- 안정 정렬 : 안정성 보장.
오름차순 과정
1) 앞에서부터 현재 값과 바로 다음의 값을 비교
2) 현재 값이 다음 값보다 크면 값을 교환 / 크지 않으면 교환X
3) 다음 값으로 이동하여 해당 값과 그다음값을 비교
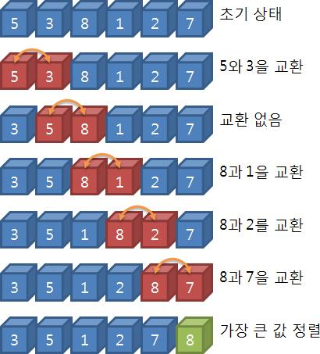
그림을 정리해보자면
한 칸씩 이동을 하며 비교를 하고, 큰 값을 오른쪽 자리로 이동시키다 보면 1회 차가 지나고 나면 가장 큰 값이 가장 오른쪽에 가있게 된다!! == 그 말은 즉, 한 회차가 지날수록 검사해야 하는 범위가 한 칸씩 줄어든다는 것.
💦 이를 배열로 생각해 보면 ~~~~~>
각 회차를 진행할 때마다 뒤에서부터 정리가 됨. 배열 크기가 [6]인 배열의
총회차는? 5회차, 즉 (배열크기-1) 회가 진행되고,
각 회차별 비교 횟수는? 1회 차> 5회, 2회 차>4회, 3회 차>3회... , 즉 (배열크기 - 회차) 번이다.
구현하기.
public class Bubble_Sort {
public static void bubble_sort(int[] a) {
bubble_sort(a, a.length);
}
private static void bubble_sort(int[] a, int size) {
// 회차는 (배열크기-1)회
for (int i=0; i<size-1; i++) {
// 회차별 비교횟수는 배열[0]부터 (배열크기-회차수)까지만
for (int j=0; j< size-i; j++) {
// 현재 값과 다음 값을 비교하여 현재 값이 크면 위치 교환
if (a[j] > a[j+1]) { //자리바꾸기
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
}
++ 추가적으로 만약 각 회차에서 비교수행을 할 때 값이 교환되지 않는다면!?
이미 정렬된 데이터라는 뜻
즉, 이 교환 정보를 판단할 수 있는 변수를 두면 불필요한 반복 비교를 막을 수 있다. > 이것이 best!!
public class Bubble_Sort {
public static void bubble_sort(int[] a) {
bubble_sort(a, a.length);
}
private static void bubble_sort(int[] a, int size) {
// 회차는 (배열크기-1)회
for (int i=0; i<size-1; i++) {
// 비교 확인 변수 설정
boolean swapCheck = false;
// 회차별 비교횟수는 배열[0]부터 (배열크기-회차수)까지만
for (int j=0; j< size-i; j++) {
// 현재 값과 다음 값을 비교하여 현재 값이 크면 위치 교환
if (a[j] > a[j+1]) { //자리바꾸기
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
swapCheck = true; // 자리를 바꿨다면 변수를 true로 변경
}
}
// 비교확인 변수가 false면 굳이 정렬을 훑을 필요가 없으므로 break문
if (swapCheck==false) {
break;
}
}
}'Coding test > Algorithm' 카테고리의 다른 글
| DP(Dynamic Programming) (2) | 2023.12.28 |
|---|---|
| Brute Force / 순열 / 조합 / 멱집합 (1) | 2023.12.17 |
| Queue 큐 / LinkedList / BFS (3) | 2023.12.07 |
| 정렬 Sorting (버블/선택/카운팅/이진 탐색) (2) | 2023.12.05 |
| 알고리즘 (3) | 2023.12.04 |













