Tree
- 원소들 간에 1:N 관계를 가지는 비선형 자료구조
- 상위 원소와 하위 원소의 관계가 있는 계층적 자료구조
1. 정의
: 한 개 이상의 노드로 이루어진 유한 집합.
- 노드/정점 : 각각 데이터를 담고 있는 원소
- 루트 노드 : 노드 중 최상위 노드
- 각 노드는 0개 이상의 자식 노드를 가질 수 있음.
- 하나의 부모에 여러 자식이 연결
- 하나의 자식은 둘 이상의 부모 X
- 노드의 갯수가 N개일 때, N-1개의 간선을 가지고 있음. -> 그래서 순환 구조가 생기지 않음.
(cf. Graph는 순환 구조가 있음.)

- 형제 노드 : 같은 부모 노드를 가진 자식 노드들
- 조상 노드 : 간선을 따라 루트 노드까지 가는 경로의 모든 노드들


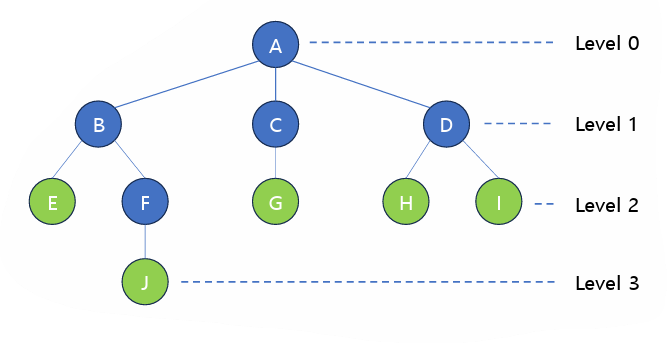
- 차수 (Degree) : 노드에 연결된 자식 노드의 수
ex) A의 차수 : 3, B의 차수: 2
- 트리의 차수 : 트리 노드들의 차수 중 제일 큰 값
- 높이 (Level) : 루트에서 노드에 이르는 간선의 수
ex)
- 트리의 높이 : 노드 중 높이가 가장 큰 값
2. 이진 트리 (Binary Tree)
: 트리 중에서 모든 부모 노드가 최대 2개의 자식 노드를 가진 트리
- 높이가 H인 이진 트리에서
> 레벨이 i인 노드의 갯수는 최 2^i
> 트리 전체의 노드의 최소 갯수는 H+1
> 최대 갯수는 2^(H+1) -1
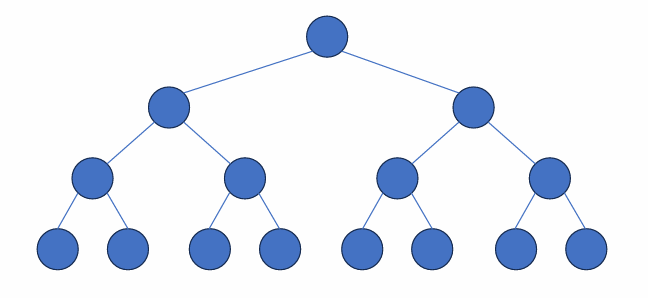
1) 포화 이진 트리 (Perfect Binary Tree)
: 모든 레벨에 노드가 최대로 차 있는 이진 트리
- 높이가 H인 트리에서 최대 노드 갯수 : 2^(H+1) -1
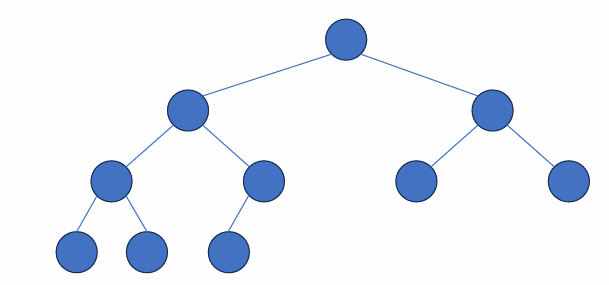
2) 완전 이진 트리 (Complete Binary Tree)
: 제일 깊은 레벨을 제외한 레벨에 노드의 갯수가 최대로 차 있으며, 마지막 레벨에 노드가 존재할 경우 왼쪽부터 차례대로 채워 넣어진 이진 트리
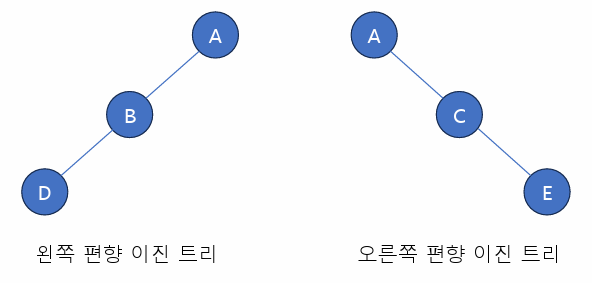
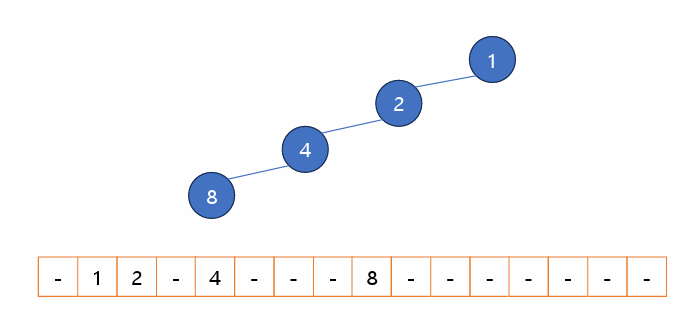
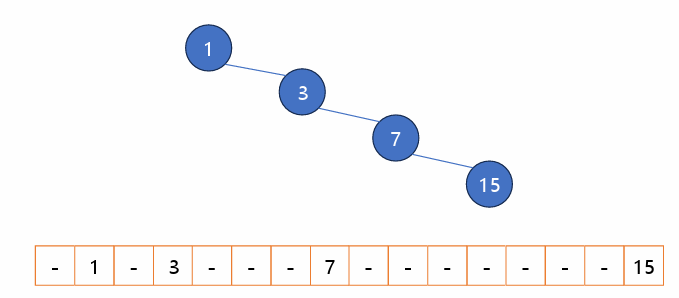
3) 편행 이진 트리 (Skewed Binary Tree)
: 높이가 H일 때 이진 트리가 가질 수 있는 최소의 노드 갯수를 가지며, 한쪽 방향의 자식 노드만 가진 이진 트리
4) 이진 트리 배열로 표현하기
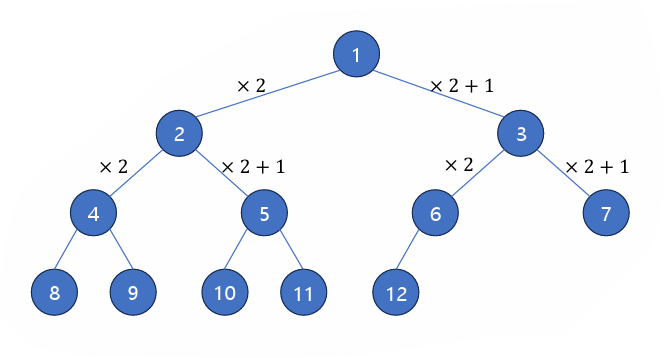

- 왼쪽 자식 노드 : i x 2
- 오른쪽 자식 노드 : i x 2 + 1
- 부모 노드 : i / 2 (소수점 버림)
** 편향 이진 트리의 경우 사용하지 않는 경우가 많다.
3. 이진 트리 순회
: 이진 트리의 각 노드를 한 번씩만 방문하는 체계적인 방법
- 루트 노드(V), 왼쪽 서브트리 (L), 오른쪽 서브트리 (R)을 정해진 순서대로

1) 전위 순회 (VLR)
: 루트 노드 -> 왼쪽 서브트리 -> 오른쪽 서브트리
ex) 1 2 4 8 9 5 10 11 3 6 12 7
2) 중위 순회 (LVR)
: 왼쪽 서브트리 -> 루트 노드 -> 오른쪽 서브트리
ex) 8 4 9 2 10 5 11 1 12 6 3 7
3) 후위 순회 (LRV)
: 왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트 노드
ex) 8 9 4 10 11 5 2 12 6 7 3 1
public class TreeArray {
// 이진 트리는 배열로 표현이 가능하다.
// 총 노드의 개수
private int nodes;
//실제 트리를 담고있는 배열
private int[] arr;
//배열을 담는다.
public void setArr(int[] arr) {
this.arr = arr;
this.nodes = arr.length;
}
// 전위순회 : VLR
// node : 현재 트리의 루트 노드 index
public void traversePreorder(int node) {
// node가 배열을 벗어나지 않고,
// 데이터가 저장되어 있다 (0이 아니다)
if (node < nodes && arr[node] != 0) {
// V방문
System.out.print(arr[node] + ", ");
// L방문
this.traversePreorder(node * 2);
// R방문
this.traversePreorder(node * 2 + 1);
}
}
// 중위순회 : LVR
public void traverseInorder(int node) {
// node가 배열을 벗어나지 않고, 데이터가 저장되어 있을 때
if (node < nodes && arr[node] != 0) {
// L방문
this.traverseInorder(node * 2);
// V방문
System.out.print(arr[node] + ", ");
// R방문
this.traverseInorder(node * 2 + 1);
}
}
// 후위순회 : LRV
public void traversePostorder(int node) {
// 조건은 동일
if (node < nodes && arr[node] != 0) {
// L방문
this.traversePostorder(node * 2);
// R방문
this.traversePostorder(node * 2 + 1);
// V방문
System.out.print(arr[node]+", ");
}
}
public static void main(String[] args) {
TreeArray tree = new TreeArray();
tree.setArr(new int[]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12});
tree.traversePreorder(1);
System.out.println(" ");
tree.traverseInorder(1);
System.out.println(" ");
tree.traversePostorder(1);
}
}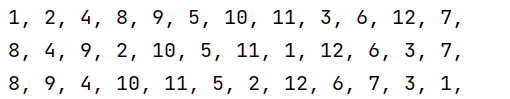
4. 이진 탐색 트리 (Binary Search Tree)
: 탐색 작업을 효율적으로 하기 위한 자료구조.
- 모든 노드의 데이터가 서로 다른 이진 트리. + 왼쪽 자식의 데이터는 모두 부모보다 작고, 오른쪽 자식의 데이터는 모두 부모보다 크다.
: 루트 노드 기준으로
- 왼쪽 서브트리의 모든 데이터는 루트 노드보다 작다.
- 오른쪽 서브트리의 모든 데이터는 루트 노드보다 크다.
- 중위 순회할 경우 오름차순 정렬된 데이터를 얻을 수 있다.
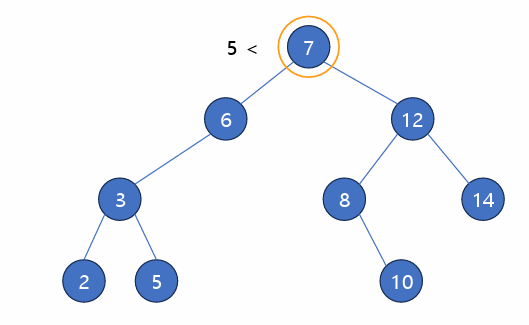
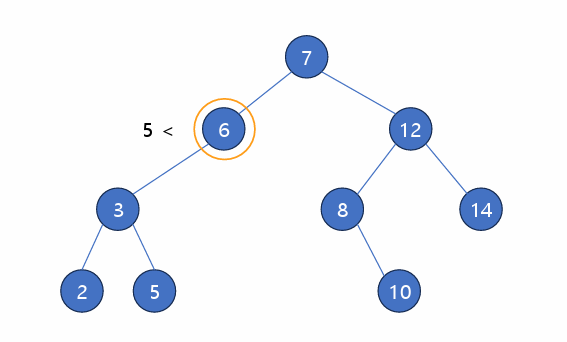
1) 탐색
- 루트 노드와 탐색 데이터 비교
- 데이터가 더 작을 경우 왼쪽 서브트리로
- 데이터가 더 클 경우 오른쪽 서브트리로
- 시간복잡도 : O(h) ~ O(logN)
- 편향 이진 트리의 경우 : O(N)


2) 삽입
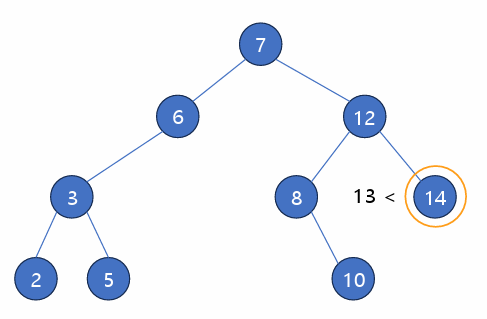
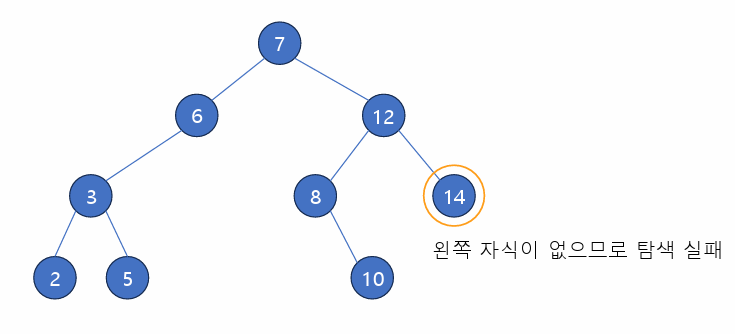
- 탐색 과정을 따라간다.
- 탐색에 성공한 경우 삽입 불가
- 탐색에 실패하는 시점에 새로운 노드로 데이터 추가



3) 삭제
- 삭제할 데이터를 가진 노드를 탐색
- 삭제할 노드가 단말 노드면 삭제 (링크 해제)
- 삭제할 노드에 자식이 하나일 경우 - 부모와 대신 연결
- 삭제할 노드에 자식이 두개일 경우, 왼쪽 서브트리의 값 중 제일 큰 노드/ 오른쪽 서브트리의 값 중 제인 작은 노드 중 하나와 교체
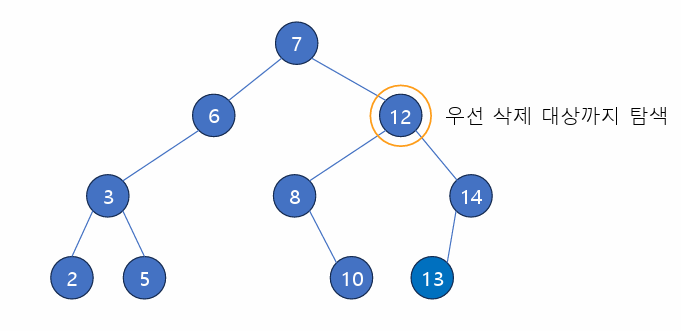
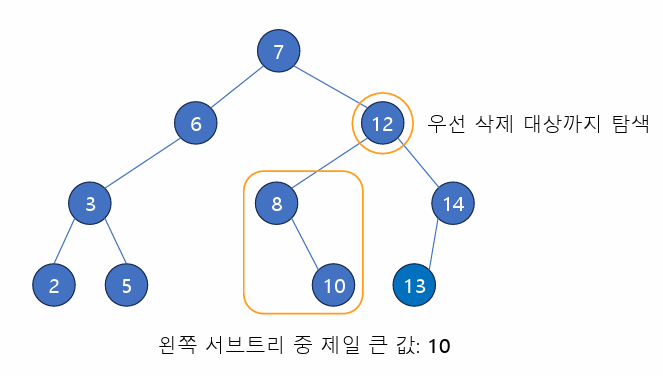

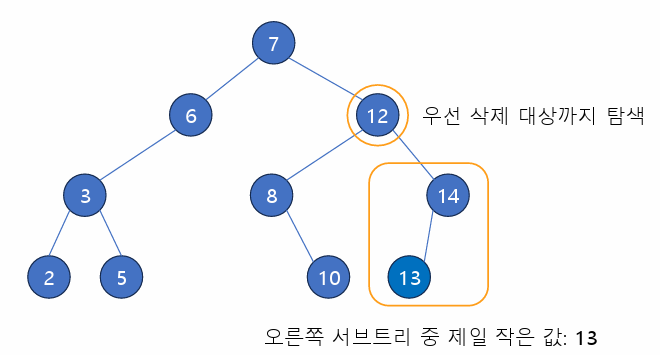

구현
public class BinarySearchTree {
// 트리의 노드를 나타내는 클래스
private static class Node {
// 담고 있는 데이터
int key;
// 왼쪽 자식
Node left;
//오른쪽 자식
Node right;
public Node(int key) {
this.key = key;
left = null;
right = null;
}
}
// 루트 노드
private Node root;
// 데이터 추가
// 데이터를 탐색해서 실패위치에서 새로운 노드를 만들어서 데이터 추가
public void insert(int key) {
root = insertNode(root, key);
}
private Node insertNode(Node node, int key) {
// 탐색 실패하는 경우 새 노드를 만든다.
if (node == null) {
node = new Node(key);
return node;
}
// 현재 노드보다 데이터가 작을 경우 왼쪽 노드를 확인
if (key < node.key) {
node.left = insertNode(node.left, key);
} //현재 노드보다 데이터가 클 경우 오른쪽 노드를 확인
else if (key > node.key) {
node.right = insertNode(node.right, key);
} return node;
}
// 탐색
public boolean search(int key) {
return searchNode(root, key);
}
private boolean searchNode(Node node, int key) {
// 현재 노드가 없을 경우 탐색 실패
if (node == null) {
return false;
}
// 현재 노드의 데이터와 일치하는 경우 탐색 성공
if (node.key == key) {
return true;
}
// 현재 노드보다 데이터가 작을 경우 왼쪽으로
// 현재 노드보다 데이터가 클 경우 오른쪽으로
if (key < node.key) {
return searchNode(node.left, key);
} else {
return searchNode(node.right, key);
}
}
public void traverseInorder() {
inorder(root);
}
private void inorder(Node node) {
if (node != null) {
inorder(node.left);
System.out.print(node.key + " ");
inorder(node.right);
}
}
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree();
bst.insert(50);
bst.insert(30);
bst.insert(70);
bst.insert(20);
bst.insert(40);
bst.insert(60);
bst.insert(80);
bst.traverseInorder();
System.out.println();
System.out.println(bst.search(40));
System.out.println(bst.search(85));
System.out.println(bst.search(30));
}
}
'Coding test > Algorithm' 카테고리의 다른 글
| Divide & Conquer 분할 정복 (0) | 2024.03.12 |
|---|---|
| Heap (0) | 2024.03.07 |
| 이항 계수 (0) | 2023.12.29 |
| DP(Dynamic Programming) (0) | 2023.12.28 |
| Brute Force / 순열 / 조합 / 멱집합 (1) | 2023.12.17 |













