Heap
- 특수한 형태의 완전 이진 트리
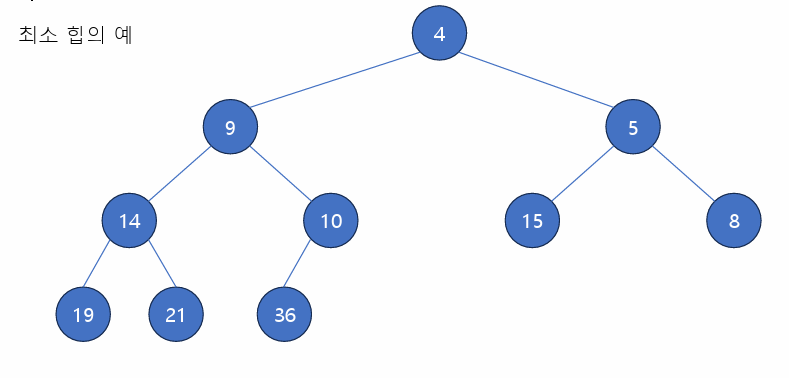
1. Heap
- 완전 이진 트리의 어떤 노드 C와 부모 노드 P가 있을 때 C의 값보다 P의 값이 항상 크거나 / C의 값보다 P의 값이 항상 작을 때.
- 다양한 요소를 가지고 있는 집합에 대하여 가장 큰 값이나 가장 작은 값을 찾기 용이함.
- 우선순위 큐를 만드는데 유용하게 사용됨.

1) 힙 삽입 연산
- 제일 오른쪽 아래에 원소를 삽입
- 새로 삽입한 원소를 부모 노드와 비교 (힙의 조건을 만족시키지 못하게 배치된 경우 서로 교환)
- 새로 추가한 원소가 루트 원소가 되거나, 힙의 조건을 만족시킬 때까지 반복
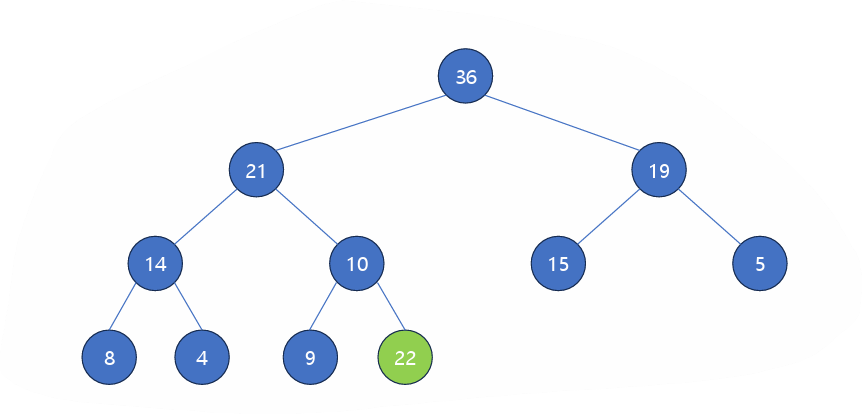





2) 힙 삭제 연산
- 힙의 루트 원소를 제거
- 루트 원소의 위치에 힙의 마지막 원소를 배치 (완전 이진트리 조건)

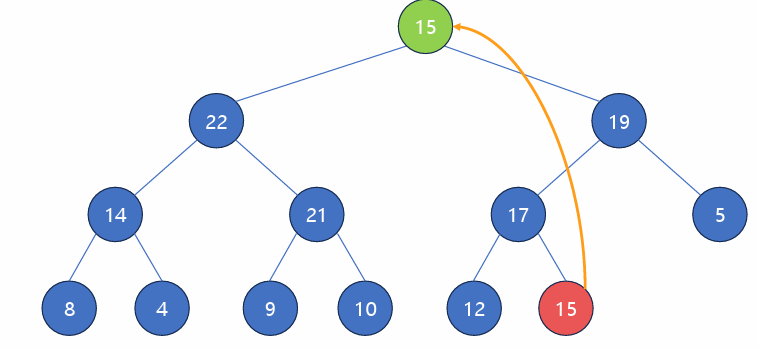
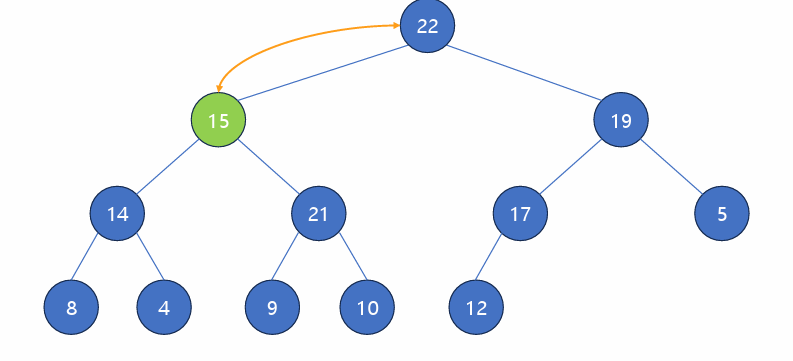

2. Heap Sort
: Heap의 특성을 사용해서 정렬하는 알고리즘.
- 그냥 힙에 다 넣었다가 뺀다..
- 주어진 배열을 최대 힙으로 변환한 다음, 제일 큰 원소를 반복해서 뒤로 보낸다.
- 추가 데이터 할당이 필요 없음.
- 시간복잡도 : O(n log n)

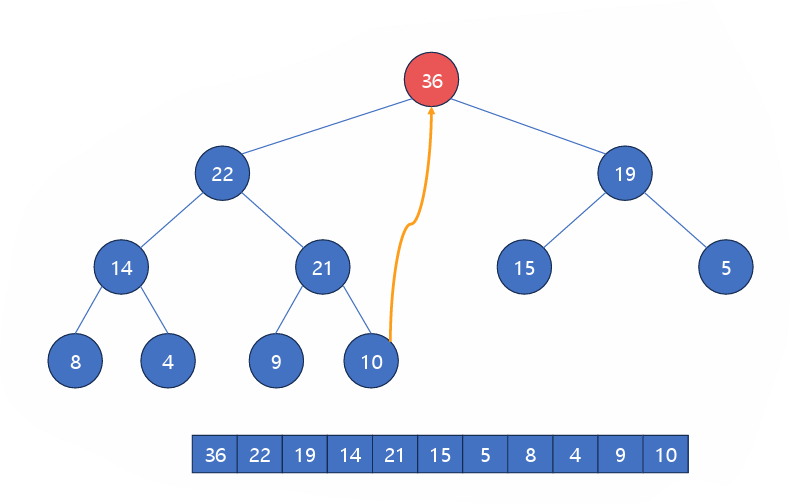

36을 빼고, 10을 넣고 36을 배열 맨 뒤로 보낸다.

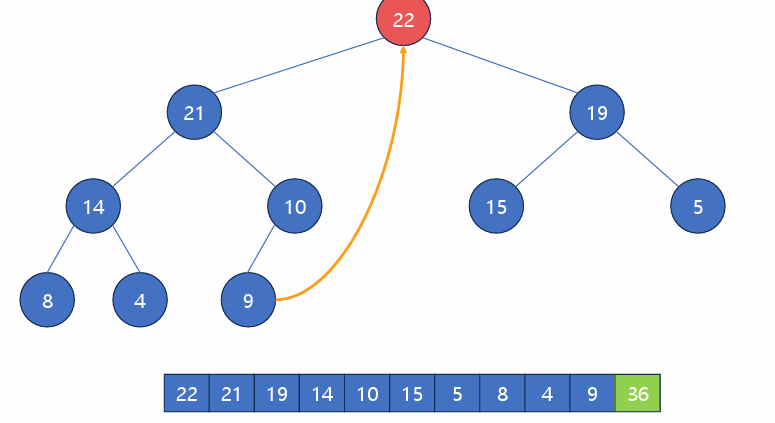
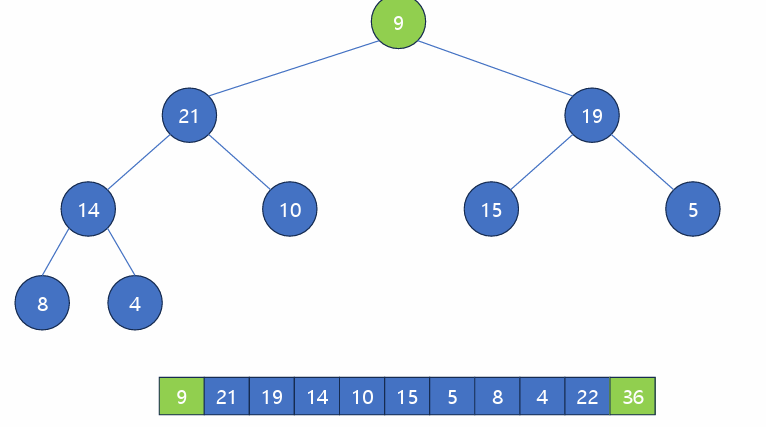
루트 원소10을 자식 원소들과 비교하여 힙의 조건을 만족시키도록 교환.
다시 루트 원소가 된 최댓값 22를 빼면서 9를 넣고, 22는 배열 맨 뒤로 보낸다.


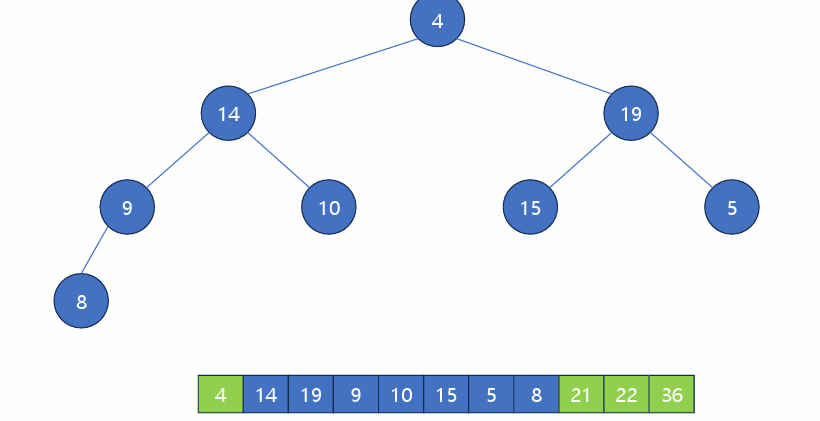
루트 원소9를 자식 원소들과 비교하여 힙의 조건을 만족시키도록 교환.
다시 루트원소가 된 최댓값 21을 빼면서 4를 넣고 21은 배열 맨뒤로 보낸다. ... 계속 반복하다보면 뒤에서부터 최댓값부터 정렬되어 순서대로 정렬되게 된다.
3. Heapify
: 주어진 배열을 힙의 형태로 변환하는 과정
- 자식을 가지고 있는 가장 높은 레벨의 노드의 위치부터 시작
- 노드와 자식 노드들의 관계가 힙 속성을 만족하도록 교환을 진행 (siftDown)
- 이후 보다 상위 노드들에서 반복
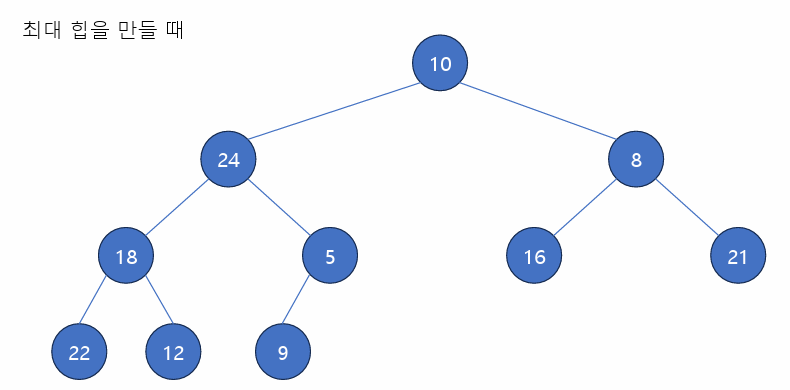


5-9 힙 속성을 만족하도록 교환
18-12 교환 불필요, 18-22 교환 필요
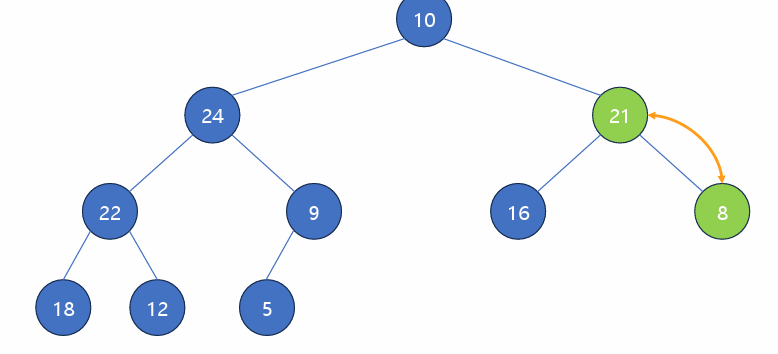
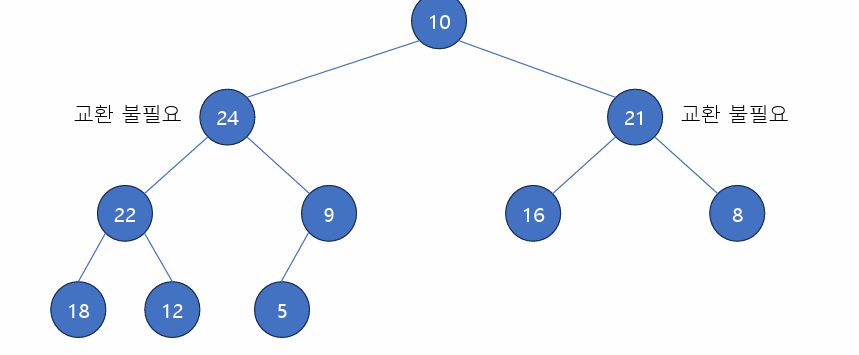

8-21 교환
21-16 교환 불필요, 24-9 교환 불필요 24-22 교환 불필요
10-24 교환
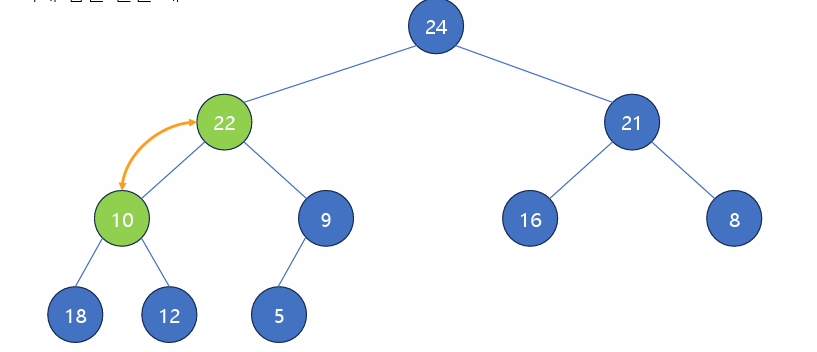
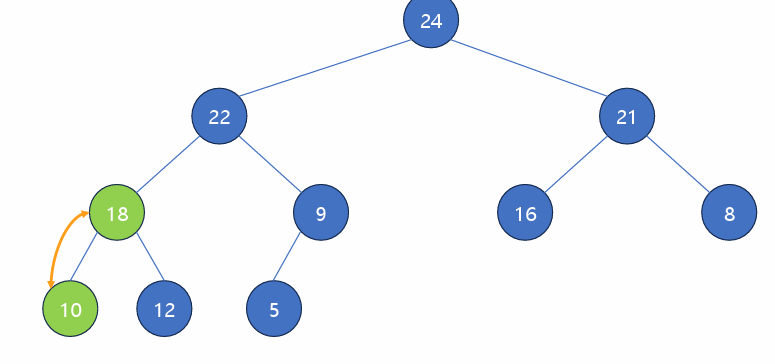
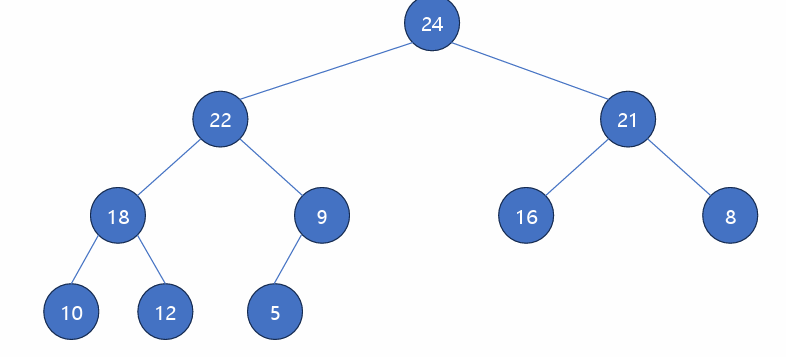
10-22 교환, 10-18 교환
'Coding test > Algorithm' 카테고리의 다른 글
| Divide & Conquer 분할 정복 (0) | 2024.03.12 |
|---|---|
| Tree (0) | 2024.03.07 |
| 이항 계수 (0) | 2023.12.29 |
| DP(Dynamic Programming) (0) | 2023.12.28 |
| Brute Force / 순열 / 조합 / 멱집합 (1) | 2023.12.17 |














